Development and Implementation of Decision Variables for Bridges within Transportation Network Systems - 2562005

Project Title—ID Number	Development and Implementation of Decision Variables for Bridges within Transportation Network Systems - 2562005
Start/End Dates	10/1/05 – 9/30/06
Funding Source	PEER-NSF
Project Leader (boldface) and Other Team Members	Anne Kiremidjian (Stanford/F), Renee Lee (Stanford/GS), Evangelos Stergiou (Stanford/GS)

Project goals and objectives

The objectives of the project are to:

• - Include the uncertainty in replacement cost and damage factor arising from the transformation from damage state to damage factor.
• - Explore methods for computing the probability distribution of loss from an ensemble of bridges without numerical integration or simulation.
• - Estimate the total loss due to components damage and network disruption using the above formulations.
• - Assess the behavior transportation networks for several earthquake scenarios
• - Account for uncertainty in component loss (sL) for a spatially distributed transportation network arising from
  • - Ground Motion Correlation
  • - Damage Correlation

Role of this project in supporting PEER's mission (vision)

This project is part of the transportation demonstration project within PEER. It integrates the various components of performance based earthquake engineering as it applies to transportation network components and systems while advancing the science in risk analysis.

Methodology employed

Under this project the correlation model for spatially dependent ground motion and bridge damage was formulated. Data from the San Francisco Bay Area was used to estimate the correlation coefficients whenever possible. In addition, a complete convolution formulation was developed for the PEER loss estimation equation. The developments are summarized as follows:

1. Probability of Loss Evaluation for an Ensemble of Bridges General Formulation of the PEER methodology

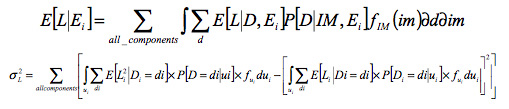
The formulation of the PEER methodology is enhanced to include the uncertainty in replacement cost, RC, and the transformation from damage state, DS, to damage factor, DF, where DF is treated as a single valued constant. The new equation is listed below:

Closed form solutions of this integral cannot be obtained. Most current approaches use numerical integration or simulation to estimate the probability of loss exceedence. In addition when computing the loss from all bridges, the total loss is

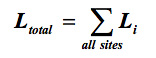
where Li is the loss from the bridge at site i. Previous applications were limited to computing the mean and variance of the total loss L. Estimation of the probability distribution of total loss requires the convolution of the losses from individual bridges. If ƒ_i is the probability density function of loss for bridge i, then the convolution is given by

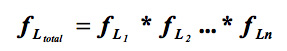
Algorithms for computing the convolution integral with limited number of bridges were developed under this project. The algorithm transforms the probability densities into the frequency domain using the Fourier transformation. In the frequency domain the transformed distributions can then be multiplied and inverse transformed to obtain the distribution of total loss.

2. Loss Evaluation With Correlation Effects

Two sources of correlation were considered. These include the correlation of ground motion at bridge sites that have similar soil type classification and the damage correlation among bridges of similar structural type, year of construction and thus design specifications.

• - Ground Motion Correlation: Two cases are investigated for ground motion correlation. We first present the case of anisotropic - distance dependent ground motion correlation. The correlation structure for this case is:
  

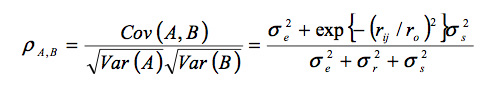
  Where r_A,B is the correlation between sites A and B, Cov(A,B) is the covariance between the two sites, Var(A) and Var(B) are the respective variances. r_ij is the distance between sites A and B and r₀ is a base distance.

  For the isotropic - distance independent correlation the formulation is given as follows:


• - The structure to structure damage correlation is expressed as
  

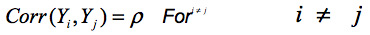
These formulations were used in sensitivity analysis for a set of bridge sites and bridge sites within the San Francisco Bay Area.

Brief Description of previous year's achievements, with emphasis on accomplishments during last year (Year 8)

A sample application was tested on 9 bridges for the San Andreas 8.0 scenario. The loss curves for each of the bridges were defined according to the enhanced equation which takes into consideration the uncertainty in replacement cost and damage factor discritization. The curves were aggregated under the independence assumption. Loss estimates for this scenario are summarized below:

• - The total value of the bridges is $6.75 M
• - Direct summation of expected values gives $5.41 M
• - Using convolution of loss curves assuming that RC, DF are constant provides an expected value of loss $3.48 M
• - Using convolution of loss curves for variable RC, DF has expected value $3.92 M

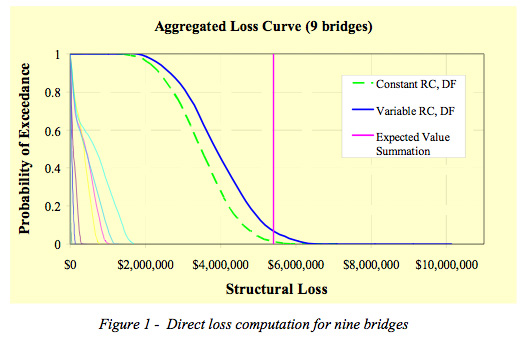
The figure above shows the probability distributions of exceeding the direct loss with constant values of RC and DF, variable RC and DF, Expected value simple summation and convolution of these distributions.

The correlation of ground motion and bridge damage was investigated through sensitivity studies. First the joint exceedence probabilities were computed for two sites with correlated ground motions. Figure 2 shows the effect of correlation on ground motion as a function of the correlation coefficients and the number of sites. It can be observed that the uncertainty in total loss computation increases significantly with the increase in number of sites and the ground motion correlation coefficient.

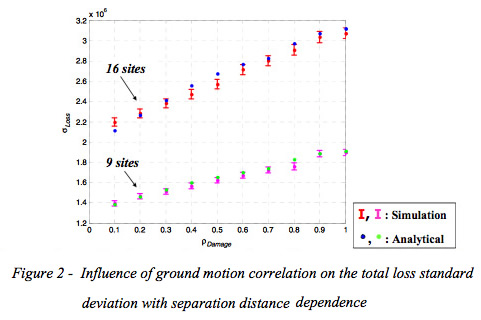
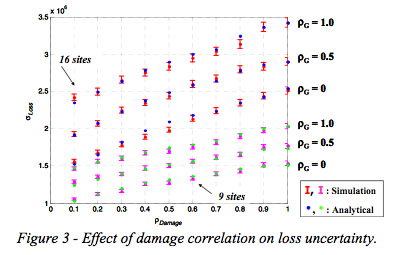
Figure 3 shows the results of the sensitivity analysis of loss standard deviation as a function of the damage correlation and the number of bridges in the system.

Other similar work being conducted within and outside PEER and how this project differs

Part of the results reported here was supported through a grant from the UPS Foundation provided by Stanford University. These results could not have been obtained solely with the support of the PEER project.

Describe any instances where you are aware that your results have been used in industry

Currently, the convolution integration of total aggregate loss is being investigated for possible adoption by Guy Carpenter Insurance Company for their portfolio risk management.

Expected milestones & deliverables

• - The following milestones and deliverables remain for the rest of this project:
• - Application of the correlation to a network
• - Estimation of probability distribution of losses for a network
• - Development of the formulation for network performance with correlated ground motion and damage functions and its effect on travel time.
• - Sample applications of these methods on a scaled down network within the San Francisco Bay Area.