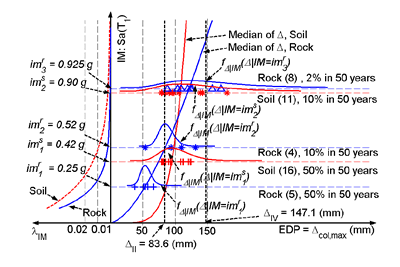
Fig. 2. Probabilistic response analysis conditioned on IM
F=faculty; GS=graduate student; US=undergraduate student; PD=post-doc; I=industrial collaborator; O=other
Click on images to enlarge in a new window
This project will contribute to the development, assessment and validation of the PEER PBEE methodology and related analytical tools through their application to a bridge structure with real-world complexities.
This project is based on advanced numerical modeling of the HBMC Bridge testbed using OpenSees. Soil, foundation, and structure are all modeled using state-of-the-art material models and finite elements recently developed and implemented in OpenSees by other PEER researchers. The probabilistic assessment methodology consists of integrating probabilistic seismic hazard analysis, nonlinear seismic response analysis of the bridge structure-foundation-soil system performed using OpenSees, and probabilistic capacity analysis (or fragility analysis) for discrete limit-states associated to potential failure modes of the bridge, in order to assess probabilistically the seismic performance of the bridge system. Parametric investigations are performed around a representative model of the HBB system to assess the effects and relative importance of a number of system parameters as well as modeling assumptions on the bridge performance. Effects of system parameter uncertainty and modeling uncertainty on the probabilistic estimate of bridge performance are also investigated.
An alternative approach is also developed based on stochastic earthquake ground motion modeling, and finite element sensitivity and reliability analysis.
This project is based on a 2-D nonlinear model of the Humboldt Bay bridge-foundation-soil system developed in OpenSees and shown in Figure 1*. The various analytical steps of the PEER PBEE methodology, namely probabilistic seismic hazard analysis, conditional and unconditional probabilistic seismic response analysis using OpenSees, probabilistic capacity analysis (or fragility analysis), and reliability analysis have been performed for the HBMC Bridge in its as-built condition. In these analyses, the following potential failure mechanisms were considered:
Fig. 2. Probabilistic response analysis conditioned on IM
Figure 2 illustrates the results of the seismic response analysis conditioned on IM taken as the 5% damped elastic spectral acceleration at the predominant period of the bridge-foundation-soil system (T1 = 1.25 sec). This figure focuses on the system level EDP defined as the maximum over all piers of the maximum tangential drift (Dcol,max) and shows the simulated values and estimated probability distributions (given IM) of Dcol,max for the three ensembles of free field ground motion time histories representing the three hazard levels (50%, 10%, and 2% probability of exceedance in 50 years). Each ensemble of earthquake records is sub-divided into soil and rock records, which require a different analytical treatment in the PEER PBEE methodology. Figure 2 also shows the mean annual rate, 1IM, of IM exceeding level Sa(T1).
Fig. 3. Demand hazard curve for Dcol,max
The seismic demand hazard curve, 1EDP(d), for EDP = Dcol,max shown in Figure 3 is obtained by convolving the conditional probability of exceedance P[EDP>d|IM] with the seismic hazard curve, 1IM.
The probabilistic capacity models used in this study are based on existing and newly developed deterministic predictive capacity models and experimental data. For each limit-state considered, a set of experimental data was collected from previous experimental research. For each experimental data point, the experimental (or measured) over calculated (or predicted) capacity ratio is computed. For failure mechanism (1), the experimental data used to develop the fragility curves originate from 10 lap spliced column specimens (4 tested at UCSD and the other 6 tested at UCLA). The fragility curves shown in Figure 4 were obtained by fitting a Normal cumulative distribution function (CDF) to the empirical CDF defined by the 20 values (each test provides 2 data points, in the push and pull directions) of the experimental over calculated capacity ratio using the least squares method.
Fig. 4 Fragility curves for flexural failure at piers
For each of the potential failure mechanisms considered,
the mean annual rate of exceeding the k-th limit-state, 
,
is obtained by convolving the corresponding fragility curve with the demand
hazard curve,
1EDP(d). The
computational results obtained for the HBMC Bridge in the as-built condition
indicate that the most critical damage-states are the initiation (return
period from 15 to 20 years) and full development (return period from 19
to 39 years)
of the shear keys failure mechanism, followed by flexural yielding in the
lap-spliced region at the base of the bridge piers (return period of 40
years).
An algorithm has been developed for finite element response sensitivity analysis of soil domains modeled using the pressure independent multi-yield-surface constitutive model used extensively in modeling the HBMC bridge ground system. This algorithm has been implemented successfully in the Opensees framework for finite element sensitivity analysis.
*(Figure 1 not included with report)
Some work has been conducted outside PEER on some individual aspects (e.g., fragility analysis of bridge components) of this project. However, to our knowledge, the integration of seismic hazard analysis, seismic demand analysis of a bridge structure-foundation-soil system, and probabilistic capacity analysis (or fragility analysis) has not been achieved outside PEER. We are and will keep reviewing the literature to identify and possibly take advantage of related work outside PEER.
Our industry partner, LAN Engineering, has expressed high interest in applying some aspects of our work in their practice, namely probabilistic seismic hazard analysis, fragility or damage analysis, and loss analysis.
Documentation of: